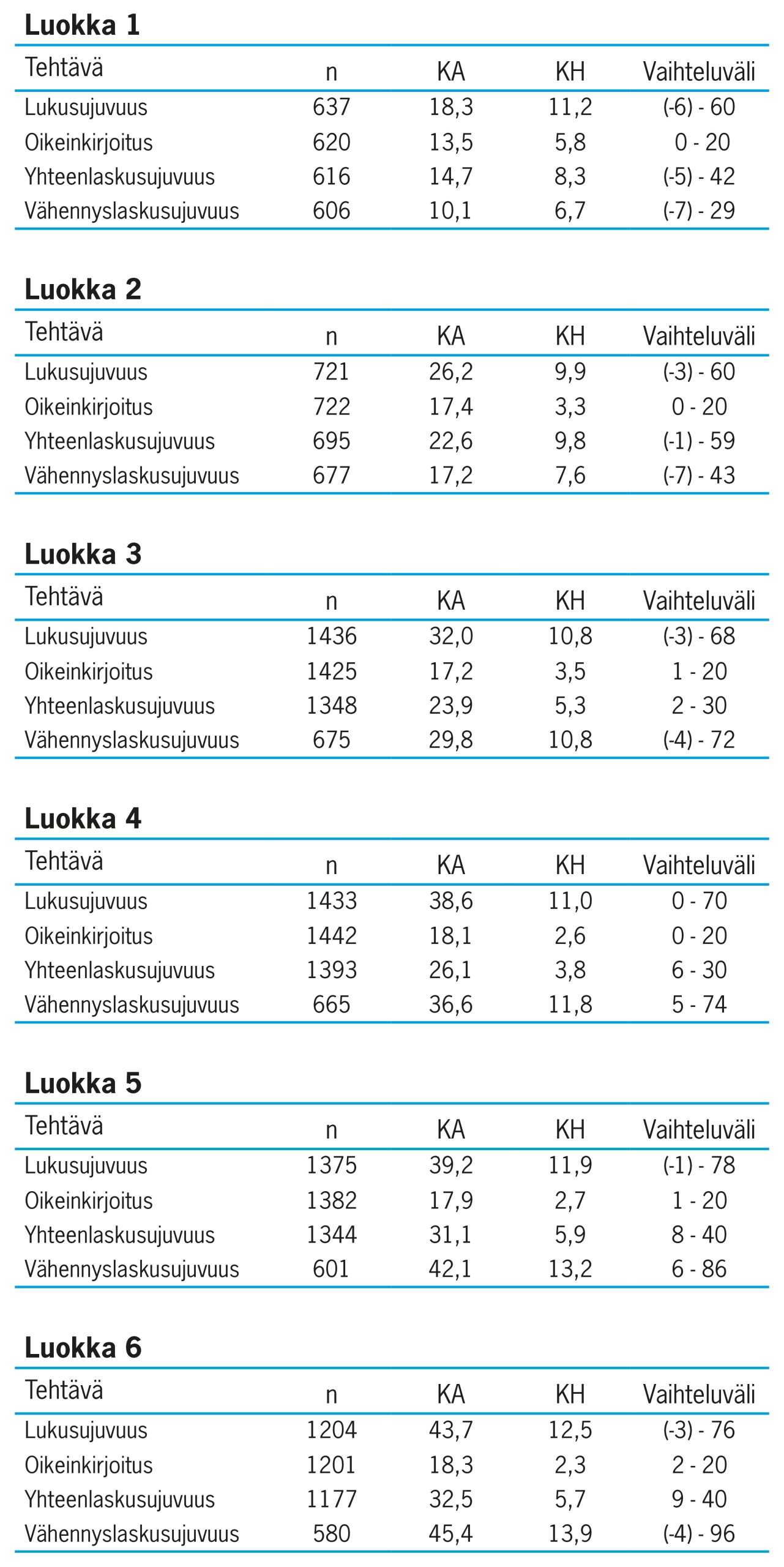
Tunnusluvut. Taulukoissa 4.7-4.12 on esitetty seulontatehtävien tunnusluvut kullakin luokka-asteella. Taulukossa n kuvaa otokseen osallistuneiden oppilaiden lukumäärää, KA kuvaa keskiarvoa ja KH keskihajontaa. Keskiarvo (KA) saadaan, kun lasketaan yhteen kaikkien oppilaiden pistemäärä kussakin tehtävässä ja jaetaan se tehtävän tehneiden oppilaiden määrällä (n). Keskiarvo kertoo siis siitä, miten tehtävässä on kullakin luokalla keskimäärin suoriuduttu. Keskihajonta (KH) kuvaa sitä, minkä verran oppilaiden tulokset keskimäärin poikkeavat keskiarvosta. Jos hajonta on pieni, suurin osa vastauksista sijoittuu lähelle keskiarvoa. Vaihteluväli kertoo otoksen pienimmän ja suurimman pistemäärän eli välin, jolle oppilaiden vastaukset sijoittuvat.
Lukusujuvuuden (Luksu) ja peruslaskusujuvuuden (Matsu) pistemäärät on laskettu vähentämällä oikeiden vastausten lukumäärästä väärien vastausten lukumäärä, jotta arvaamalla ei voi saada korkeaa pistemäärää. Tehtävissä on kuitenkin keskimäärin tehty hyvin vähän virheitä (ks. alla).
Taulukot 4.7-4.12.: Tehtävien tunnusluvut
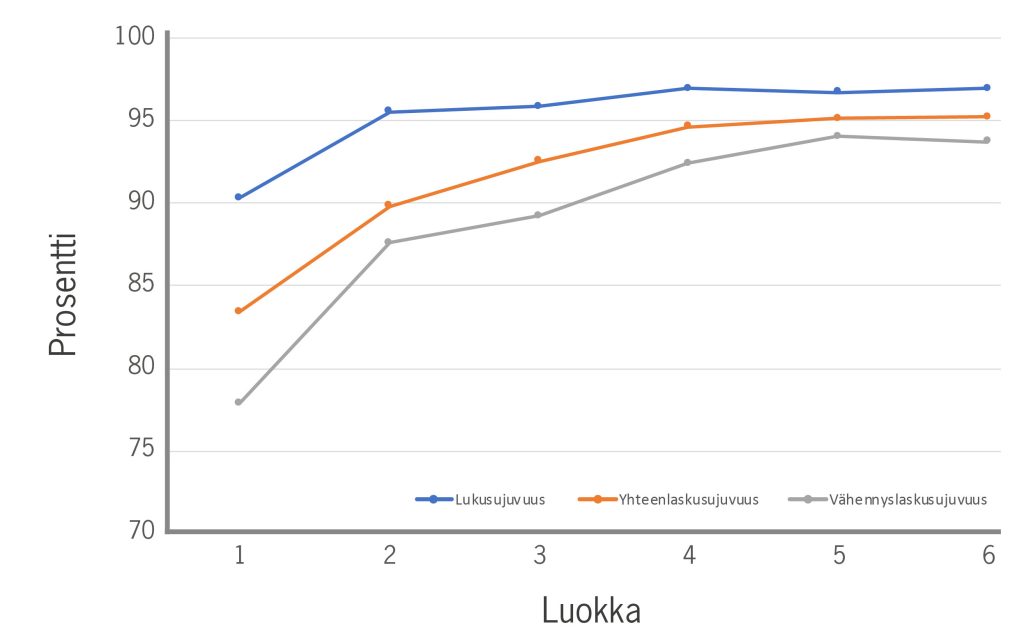
Virheet. Kuvaajassa 4.1 kuvataan tiivistetysti aikarajallisten tehtävien (Luksu, Matsu) oikeellisuusprosenttia kullakin luokalla. Kuten kuvaajasta näkyy, kaikissa tehtävissä tehdään toisesta luokasta lähtien vain hyvin vähän virheitä: lukusujuvuudessa keskimäärin yli 95 % vastauksista on oikein, yhteenlaskusujuvuudessa yli 90 % ja vähennyslaskusujuvuudessakin lähes saman verran. Ensimmäisellä luokalla virheitä tehdään prosentuaalisesti enemmän, mikä kertoo siitä, että taito on vielä kehittymässä. Näissä sujuvuustehtävissä tulkinnassa kannattaa keskittyä erityisesti lukemisen ja laskemisen nopeuteen, mutta runsaaseen virheiden määrään kannattaa toki kiinnittää huomiota. Karkeasti ottaen voisi sanoa, että jos oppilas tekee yli 5 virhettä sujuvuustehtävässä, tulosta kannattaa tarkastella tarkemmin.
Keskimääräinen virheiden määrä sanelu- ja täydennä tekstit -tehtävissä on laskettavissa suoraan tunnusluvuista, siksi niitä ei ole erikseen raportoitu. Esimerkiksi ensimmäisen luokan sanelussa tulee keskimäärin 6,5 virhettä (kirjoitettujen sanojen määrä, joka on kaikilla 20 vähennettynä oikeiden vastausten keskiarvo = 20 – 13,5).
Kuvaaja 4.1.: Aikarajallisten tehtävien oikeellisuusprosentit luokilla 1-6.
Tehtävien jakaumat. Tehtävien pistemäärien jakaumat on esitetty kuvioissa 4.1-4.28. Kuvioon on merkitty tulosten keskiarvo sekä väritetty alue, joka vastaa yhtä keskihajontaa keskiarvon molemmin puolin. Oppilaista noin 70 % sijoittuu tälle alueelle. Karkeasti ottaen voidaan ajatella, että oppilaat, joiden tulokset sijoittuvat tälle alueelle tai sitä paremmin, suoriutuvat tehtävistä odotetulla tavalla. Se ’häntä’, josta seulatehtävissä ollaan kiinnostuneita, sijoittuu jakauman vasempaan laitaan harmaan alueen ulkopuolelle. Seulassa huolen raja on määritelty 15 persentiiliin, joka vastaa heikointa viittätoista prosenttia tuloksista. Tämä persentiiliraja ei täsmälleen vastaa yhtä keskihajontaa (jonka ulkopuolelle jää normaalijakautuneessa otoksessa 16 %), mutta on hyvin lähellä sitä ja siksi voidaan tulkita kutakuinkin samalla tavoin. Tarkat 15 persentiilin rajat kussakin tehtävässä näkyvät taulukoissa 5.1-5.6. Kun halutaan tarkastella oppilaskohtaisia tuloksia suhteessa normiaineistoon, kannattaakin pisteitä verrata luvun 4 persentiilitaulukoihin, joiden mukaan tulokset on esitetty myös Alakoulun DigiLukiseulan palvelimella esitetyissä koonneissa opettajan käyttöliittymän kautta.
Jakaumakuvioista näkyy, että lukusujuvuuden (Luksu, kuviot 4.1-4.6) ja peruslaskutaidon sujuvuuden (Matsu yhteenlasku, kuviot 4.23-4.28) pistemäärien jakaumat noudattavat hyvin normaalijakaumaa. Sen sijaan oikeinkirjoituksen jakauma (kuviot 4.7-4.12) on ensimmäisen luokan jälkeen vahvasti vino vasemmalle. Se tarkoittaa sitä, että suurin osa oppilaista osaa kirjoittaa lähes kaikki sanat oikein, ja vain pieni osa oppilaista jää selvästi kauemmas keskiarvosta. Tämä vaikuttaa myös keskihajontaan, joka on oikeinkirjoituksessa tyypillisesti melko pieni. Oikeinkirjoittamisessa erottuu kuitenkin selkeästi pitkä häntä keskiarvon alapuolella, ja tehtävä erottelee hyvin ne oppilaat, joiden oikeinkirjoitus sujuu heikosti. Tehtävä soveltuukin hyvin seulontatarkoitukseen. Täydennä tekstit -tehtävän jakaumat (kuviot 4.13-4.16) ovat myös vasemmalle vinoja, mikä kertoo siitä, että suurin osa oppilaista hallitsee luetun ymmärtämisen taidon hyvin. Myös tässä tehtävässä mielenkiinnon kohteena on erityisesti jakauman häntä, joka sisältää niiden oppilaiden tulokset, joiden luetun ymmärtämisen taito on keskimääräistä selvästi heikompi. Tehtävän erottelukyky on hyvä, eli se auttaa löytämään oppilaat, joiden luetun ymmärtämisessä on tuen tarvetta. Kaikki edellä kuvatut tehtävät soveltuvat siis hyvin seulontatarkoitukseen eli niiden oppilaiden tunnistamiseen, joiden taidot jäävät keskitasoa heikommiksi ja joiden osaamista on tärkeää arvioida tarkemmin.
Katso tästä oikeiden vastausten jakaumakuviot!
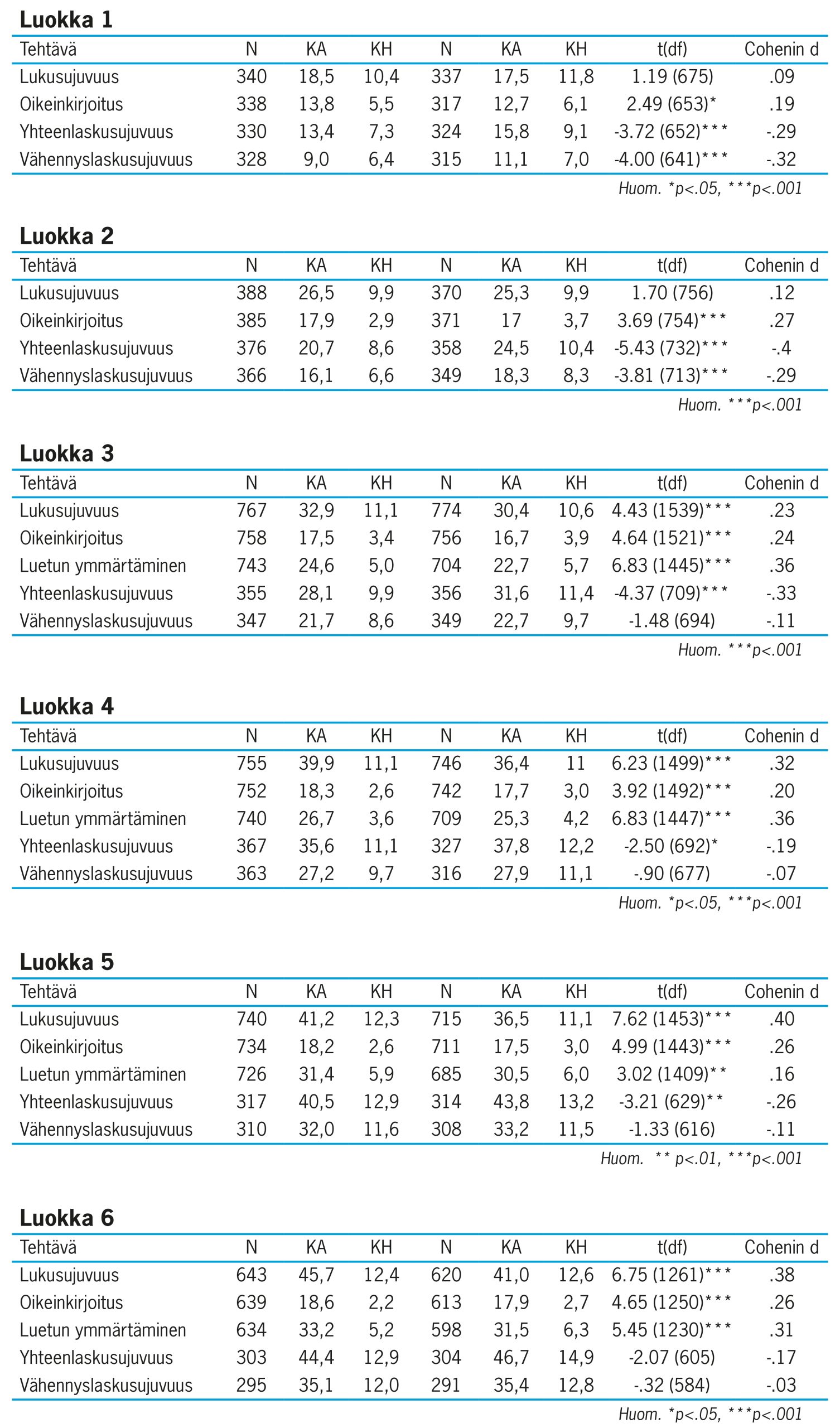
Sukupuolierot. Taulukoissa 4.13-4.18 on kuvattu tyttöjen ja poikien suoriutuminen Alakoulun DigiLukiseulan tehtävissä. Niistä käy ilmi, että kolmannelta luokalta eteenpäin tytöt suoriutuvat poikia paremmin lukusujuvuudessa ja luetun ymmärtämisessä. Oikeinkirjoituksessa ero näkyy jo ensimmäiseltä luokalta lähtien. Yhteenlaskusujuvuudessa pojat sen sijaan suoriutuvat tyttöjä paremmin ensimmäiseltä kuudennelle luokalle saakka. Vähennyslaskussa pojat ovat tyttöjä parempia ensimmäisellä ja toisella luokalla, mutta ero katoaa kolmannesta luokasta lähtien. Voidaan siis todeta, että tytöt suoriutuvat keskimäärin poikia paremmin luku- ja kirjoitustaidon tehtävissä, pojat puolestaan tyttöjä paremmin peruslaskutoimitusten sujuvuudessa, erityisesti yhteenlaskussa.
Taulukko 4.13-4.18: Tyttöjen ja poikien suoriutuminen tehtävissä